



Next: Harmonic restraints
Up: Biasing and analysis methods
Previous: Extended-system Adaptive Biasing Force
Contents
Index
Subsections
Metadynamics
The metadynamics method uses a history-dependent potential [59] that generalizes to any type of colvars the conformational flooding [60] and local elevation [61] methods, originally formulated to use as colvars the principal components of a covariance matrix or a set of dihedral angles, respectively.
The metadynamics potential on the colvars
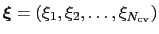 is defined as:
is defined as:
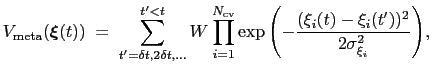 |
(13.22) |
where
 is the history-dependent potential acting on the current values of the colvars
is the history-dependent potential acting on the current values of the colvars
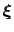 , and depends only parametrically on the previous values of the colvars.
, and depends only parametrically on the previous values of the colvars.
 is constructed as a sum of
is constructed as a sum of
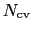 -dimensional repulsive Gaussian ``hills'', whose height is a chosen energy constant
-dimensional repulsive Gaussian ``hills'', whose height is a chosen energy constant 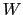 , and whose centers are the previously explored configurations
, and whose centers are the previously explored configurations
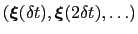 .
.
During the simulation, the system evolves towards the nearest minimum of the ``effective'' potential of mean force
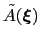 , which is the sum of the ``real'' underlying potential of mean force
, which is the sum of the ``real'' underlying potential of mean force
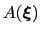 and the the metadynamics potential,
and the the metadynamics potential,
 .
Therefore, at any given time the probability of observing the configuration
.
Therefore, at any given time the probability of observing the configuration
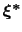 is proportional to
is proportional to
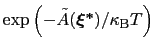 : this is also the probability that a new Gaussian ``hill'' is added at that configuration.
If the simulation is run for a sufficiently long time, each local minimum is canceled out by the sum of the Gaussian ``hills''.
At that stage the ``effective'' potential of mean force
: this is also the probability that a new Gaussian ``hill'' is added at that configuration.
If the simulation is run for a sufficiently long time, each local minimum is canceled out by the sum of the Gaussian ``hills''.
At that stage the ``effective'' potential of mean force
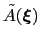 is constant, and
is constant, and
 is an accurate estimator of the ``real'' potential of mean force
is an accurate estimator of the ``real'' potential of mean force
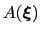 , save for an additive constant:
, save for an additive constant:
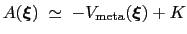 |
(13.23) |
Assuming that the set of collective variables includes all relevant degrees of freedom, the predicted error of the estimate is a simple function of the correlation times of the colvars
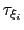 , and of the user-defined parameters
, and of the user-defined parameters 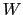 ,
,
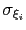 and
and 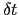 [62].
In typical applications, a good rule of thumb can be to choose the ratio
[62].
In typical applications, a good rule of thumb can be to choose the ratio
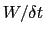 much smaller than
much smaller than
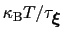 , where
, where
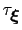 is the longest among
is the longest among
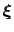 's correlation times:
's correlation times:
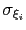 then dictates the resolution of the calculated PMF.
then dictates the resolution of the calculated PMF.
To enable a metadynamics calculation, a metadynamics block must be defined in the colvars configuration file.
Its mandatory keywords are colvars, which lists all the variables involved, and hillWeight, which specifies the weight parameter 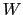 .
The parameters
.
The parameters 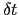 and
and
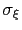 specified by the optional keywords newHillFrequency and hillWidth:
specified by the optional keywords newHillFrequency and hillWidth:
Output files
When interpolating grids are enabled (default behavior), the PMF is written every colvarsRestartFrequency steps to the file outputName.pmf.
The following two options allow to control this behavior and to visually track statistical convergence:
Note: when Gaussian hills are deposited near lowerBoundary or upperBoundary (see 13.2.1) and interpolating grids are used (default behavior), their truncation can give rise to accumulating errors.
In these cases, as a measure of fault-tolerance all Gaussian hills near the boundaries are included in the output state file, and are recalculated analytically whenever the colvar falls outside the grid's boundaries.
(Such measure protects the accuracy of the calculation, and can only be disabled by hardLowerBoundary or hardUpperBoundary.)
To avoid gradual loss of performance and growth of the state file, either one of the following solutions is recommended:
- enabling the option expandBoundaries, so that the grid's boundaries are automatically recalculated whenever necessary; the resulting .pmf will have its abscissas expanded accordingly;
- setting lowerWall and upperWall well within the interval delimited by lowerBoundary and upperBoundary.
Performance tuning
The following options control the computational cost of metadynamics calculations, but do not affect results.
Default values are chosen to minimize such cost with no loss of accuracy.
Well-tempered metadynamics
The following options define the configuration for the ``well-tempered'' metadynamics approach [63]:
Multiple-replicas metadynamics
The following options define metadynamics calculations with more than
one replica:
-
multipleReplicas
 Multiple replicas metadynamics
Multiple replicas metadynamics
Context: metadynamics
Acceptable values: boolean
Default value: off
Description: If this option is on, multiple (independent) replica of the
same system can be run at the same time, and their hills will be
combined to obtain a single PMF [64]. Replicas are
identified by the value of replicaID. Communication is
done by files: each replica must be able to read the files
created by the others, whose paths are communicated through the file
replicasRegistry. This file, and the files listed in it,
are read every replicaUpdateFrequency steps. Every time
the colvars state file is written
(colvarsRestartFrequency), the file:
``outputName.colvars.name.replicaID.state''
is also written, containing
the state of the metadynamics bias for replicaID. In the
time steps between colvarsRestartFrequency, new hills are
temporarily written to the file:
``outputName.colvars.name.replicaID.hills'',
which serves as communication
buffer. These files are only required for communication, and may be
deleted after a new MD run is started with a different
outputName.
-
replicaID
 Set the identifier for this replica
Set the identifier for this replica
Context: metadynamics
Acceptable values: string
Description: If multipleReplicas is on, this option sets a
unique identifier for this replica. All replicas should use
identical collective variable configurations, except for the value
of this option.
-
replicasRegistry
 Multiple replicas database file
Multiple replicas database file
Context: metadynamics
Acceptable values: UNIX filename
Default value: ``name.replica_files.txt''
Description: If multipleReplicas is on, this option sets the
path to the replicas' database file.
-
replicaUpdateFrequency
 How often hills are communicated between
replicas
How often hills are communicated between
replicas
Context: metadynamics
Acceptable values: positive integer
Default value: newHillFrequency
Description: If multipleReplicas is on, this option sets the
number of steps after which each replica (re)reads the other
replicas' files. The lowest meaningful value of this number is
newHillFrequency. If access to the file system is
significantly affecting the simulation performance, this number can
be increased, at the price of reduced synchronization between
replicas. Values higher than colvarsRestartFrequency may
not improve performance significantly.
-
dumpPartialFreeEnergyFile
 Periodically write the contribution to the
PMF from this replica
Periodically write the contribution to the
PMF from this replica
Context: metadynamics
Acceptable values: boolean
Default value: on
Description: When multipleReplicas is on, the file
outputName.pmf contains the combined PMF from all
replicas, provided that useGrids is on (default).
Enabling this option produces an additional file
outputName.partial.pmf, which can be useful to
quickly monitor the contribution of each replica to the PMF.
The following options may be useful only for applications that go beyond the calculation of a PMF by metadynamics:
-
name
 Name of this metadynamics instance
Name of this metadynamics instance
Context: metadynamics
Acceptable values: string
Default value: ``meta'' + rank number
Description: This option sets the name for this metadynamics instance. While it
is not advisable to use more than one metadynamics instance within
the same simulation, this allows to distinguish each instance from
the others. If there is more than one metadynamics instance, the
name of this bias is included in the metadynamics output file names, such as e.g. the .pmf file.
-
keepHills
 Write each individual hill to the state
file
Write each individual hill to the state
file
Context: metadynamics
Acceptable values: boolean
Default value: off
Description: When useGrids and this option are on, all hills
are saved to the state file in their analytic form, alongside their
grids. This makes it possible to later use exact analytic Gaussians
for rebinGrids. To only keep track of the history of the
added hills, writeHillsTrajectory is preferable.
-
writeHillsTrajectory
 Write a log of new hills
Write a log of new hills
Context: metadynamics
Acceptable values: boolean
Default value: on
Description: If this option is on, a logfile is written by the
metadynamics bias, with the name
``outputName.colvars. name
name .hills.traj'', which
can be useful to follow the time series of the hills. When
multipleReplicas is on, its name changes to
.hills.traj'', which
can be useful to follow the time series of the hills. When
multipleReplicas is on, its name changes to
``outputName.colvars. name
name .
. replicaID
replicaID .hills.traj''.
This file can be used to quickly visualize the positions of all
added hills, in case newHillFrequency does not coincide
with colvarsRestartFrequency.
.hills.traj''.
This file can be used to quickly visualize the positions of all
added hills, in case newHillFrequency does not coincide
with colvarsRestartFrequency.




Next: Harmonic restraints
Up: Biasing and analysis methods
Previous: Extended-system Adaptive Biasing Force
Contents
Index
vmd@ks.uiuc.edu
![]() is defined as:
is defined as:
![]() , which is the sum of the ``real'' underlying potential of mean force
, which is the sum of the ``real'' underlying potential of mean force
![]() and the the metadynamics potential,
and the the metadynamics potential,
![]() .
Therefore, at any given time the probability of observing the configuration
.
Therefore, at any given time the probability of observing the configuration
![]() is proportional to
is proportional to
![]() : this is also the probability that a new Gaussian ``hill'' is added at that configuration.
If the simulation is run for a sufficiently long time, each local minimum is canceled out by the sum of the Gaussian ``hills''.
At that stage the ``effective'' potential of mean force
: this is also the probability that a new Gaussian ``hill'' is added at that configuration.
If the simulation is run for a sufficiently long time, each local minimum is canceled out by the sum of the Gaussian ``hills''.
At that stage the ``effective'' potential of mean force
![]() is constant, and
is constant, and
![]() is an accurate estimator of the ``real'' potential of mean force
is an accurate estimator of the ``real'' potential of mean force
![]() , save for an additive constant:
, save for an additive constant:
![]() , and of the user-defined parameters
, and of the user-defined parameters ![]() ,
,
![]() and
and ![]() [62].
In typical applications, a good rule of thumb can be to choose the ratio
[62].
In typical applications, a good rule of thumb can be to choose the ratio
![]() much smaller than
much smaller than
![]() , where
, where
![]() is the longest among
is the longest among
![]() 's correlation times:
's correlation times:
![]() then dictates the resolution of the calculated PMF.
then dictates the resolution of the calculated PMF.
![]() .
The parameters
.
The parameters ![]() and
and
![]() specified by the optional keywords newHillFrequency and hillWidth:
specified by the optional keywords newHillFrequency and hillWidth: