

Next: Steered Molecular Dynamics
Up: Analysis
Previous: Equilibrium
Subsections
In this section, you will analyze two non-equilibrium properties of proteins, the diffusion of heat and a phenomenon known as temperature echoes. This section requires some knowledge of the principles of statistical physics, but the results of the simulations can be understood intuitively even without a deep understanding of their principles.
For this exercise, you will use the last step of the equilibration of
ubiquitin in a water sphere, file ubq_ws_eq.restart.coor. You
will use the temperature coupling feature of NAMD to set the
temperature of the molecules in the outer layer of the sphere to
200 K, while the rest of the bubble is set to a temperature of 300 K.
In this way, you will determine the thermal diffusivity by monitoring
change of the system's temperature and comparing it to the
theoretical expression.
- * 1
- Change to this problem's directory in a Terminal window:
In order to use the temperature coupling feature of NAMD, you need to create a file which marks the atoms subject to the temperature coupling.
The following lines
| tCouple on |
|
| tCoupleTemp 200 |
|
| tCoupleFile ubq_shell.pdb |
|
tCoupleCol B
|
|
in the provided configuration file ubq_cooling.conf will enable this feature, and set the atoms coupled to the thermal bath as the ones that have a value of 1.00 in the B column of the ubq_shell.pdb, which you will create below.
- * 2
- In the VMD TkCon window, navigate to the 2-6-heat-diff/ directory.
- 3
- Load the system into VMD by typing the following
in the VMD TkCon window:
| mol new ../common/ubq_ws.psf |
|
mol addfile ../1-2-sphere/ubq_ws_eq.restart.coor
|
|
- 4
- Select all atoms in the system:
set selALL [atomselect top all]
|
|
- 5
- Find the center of the system:
set center [measure center $selALL weight mass]
|
|
- 6
- Find
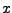 ,
, 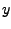 and
and 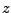 coordinates of the system's center and place their values in the variables xmass, ymass, and zmass:
coordinates of the system's center and place their values in the variables xmass, ymass, and zmass:
foreach {xmass ymass zmass} $center { break }
|
|
- 7
- Select atoms in the outer layer:
| set shellSel [atomselect top "not ( sqr(x-$xmass) |
|
+ sqr(y-$ymass) + sqr(z-$zmass) <= sqr(22) ) "]
|
|
- 8
- Set beta parameters of the atoms in this selection to 1.00:
- 9
- Create the pdb file that marks the atoms in the outer layer by ``1.00'' in the beta column:
$selALL writepdb ubq_shell.pdb
|
|
- 10
- Run the Molecular Dynamics simulation
- * 11
- If you do not run the simulation yourself, you will need to obtain the data for the temperature from the provided log file. Copy this log file from the directory example-output/.
copy example-output ubq_cooling.log . ubq_cooling.log .
|
|
If you run the simulation yourself, your log file will be generated by NAMD, and you do not need to copy it.
- * 12
- Use namdstats.tcl to find out how the system's temperature changes with time. In the VMD TkCon window, type:
| source ../2-3-energies/namdstats.tcl |
|
data_time TEMP ubq_cooling.log
|
|
The file TEMP.dat will be written with the temperature of the system over time.
- * 13
- You can now quit VMD.
- * 14
- In Excel, click File
 Open
Open , navigate to the directory 2-6-heat-diff/, and choose the file TEMP.dat. Make sure the dropdown menu Files of type is set to All Files.
, navigate to the directory 2-6-heat-diff/, and choose the file TEMP.dat. Make sure the dropdown menu Files of type is set to All Files.
- * 15
- When the Text Import Wizard appears, choose Delimited for your file type and click Next. Under the category Delimiters, click Tab. The Data Preview window should show your timestep and temperature data separated into two columns. Click Finish. The timestep and temperature values will appear in Columns A and B, respectively.
- * 16
- Before plotting the data, we will modify the time units so that they are in units of fs, not timesteps. In cell C1, type the formula =A1*2, click and hold the lower-right corner of C1 and drag down to cell C201. These values are the simulation time in fs.
- * 17
- Plot the temperature data by clicking Insert
 Chart
Chart , choosing XY (Scatter) as your Chart Type, selecting the last Chart sub-type in the lower-right, and clicking Next.
, choosing XY (Scatter) as your Chart Type, selecting the last Chart sub-type in the lower-right, and clicking Next.
- * 18
- In Step 2, click the Series tab, remove any existing series, and click the Add button. Click the red button in the X Values: field, select every data value in Column C (Rows 1-201), and click the red button to complete. Do the same for the Y Values: using the data in Column B. Click Finish.
- * 19
- Double click on the y-axis and change the Minimum: value to 200. Click OK. Modify the chart further if you wish.
- * 20
- You will now fit the simulated temperature dependence to the
theoretical expression.
- * 21
- In cell D1, type or copy and paste the formula (make sure it is on one line):
| = 200 |
|
| +66.87*(EXP(-0.0146*E$1*C1) +0.25*EXP(-0.25*0.0146*E$1*C1) |
|
| +1/9*EXP(-1/9*0.0146*E$1*C1) +1/16*EXP(-1/16*0.0146*E$1*C1) |
|
| +1/25*EXP(-1/25*0.0146*E$1*C1) +1/36*EXP(-1/36*0.0146*E$1*C1) |
|
| +1/49*EXP(-1/49*0.0146*E$1*C1) +1/64*EXP(-1/64*0.0146*E$1*C1) |
|
+1/81*EXP(-1/81*0.0146*E$1*C1) +1/100*EXP(-1/100*0.0146*E$1*C1))
|
|
The value in cell E1 is the thermal diffusivity, which we will alter to obtain a better fit. Enter an initial guess of 0.03 in cell E1. Then extend the formula in D1 down to cell D201.
- * 22
- In the chart, right-click on the temperature data and select Source Data
 . Click the Series tab and add a series with Y Values: of Column D, Rows 1-201. and X Values: of Column C. Click OK.
. Click the Series tab and add a series with Y Values: of Column D, Rows 1-201. and X Values: of Column C. Click OK.
You may want to change the line weight of your fit by right-clicking the line in your histogram and selecting Format Data Series .
.
We have our theoretical temperature expression plotted, but the fit is not optimal. If we change thermal diffusivity in cell E1, we will see the fit change. We will now determine the optimal parameters.
- * 23
- In cell F1, type the formula =(D1-B1)
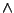 2. Then click and hold the lower-right corner of cell F1 and drag down to row 201 to fill in the error values for each bin.
2. Then click and hold the lower-right corner of cell F1 and drag down to row 201 to fill in the error values for each bin.
- * 24
- Type =sum(F1:F201) into cell G1. This is the total square error for our fit, and it is what we seek to minimize using the Solver tool.
- * 25
- Click Tools
 Solver
Solver . If that option is not present, you will need to add in the Solver tool by clicking Tools
. If that option is not present, you will need to add in the Solver tool by clicking Tools  Add Ins
Add Ins and selecting Solver Add-in from the list.
and selecting Solver Add-in from the list.
- * 26
- In the Solver Parameters window, set the following cell ranges and click Solve:
| Set Target Cell: $G$1 |
|
| Equal To: Min |
|
By Changing Cells: $E$1
|
|
Solver will find the thermal diffusivity which optimally fits the temperature expression to our raw temperature data.
Figure 13:
Cooling of ubiquitin in a water sphere. The smooth black line shows a non-linear fit of the data to the theoretical expression.
![\begin{figure}\begin{center}
\par
\par
\latex{
\includegraphics[scale=0.5]{pictures/tut_unit02_coolwin}
}
\end{center}
\end{figure}](img105.png) |
- * 27
- Multiply the value of the parameter in cell E1 by 0.1 to get the
thermal diffusivity in cm
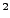 s
s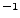 . You should get a value of around
0.45
. You should get a value of around
0.45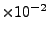 cm
cm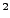 s
s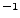 . How does your result compare
to the thermal diffusivity of water
. How does your result compare
to the thermal diffusivity of water
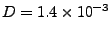 cm
cm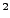 s
s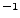 ?
?
- * 28
- Compute the thermal conductivity of the system,
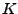 , by the following
formula:
, by the following
formula:
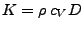 , where
, where 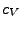 is the specific heat (that was
calculated in Section 2.1.5) and
is the specific heat (that was
calculated in Section 2.1.5) and 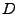 is the thermal diffusivity
(assume that the density of the system,
is the thermal diffusivity
(assume that the density of the system, 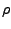 , is 1 g/mL).
, is 1 g/mL).
- * 29
- Save the file you created in Excel if you wish, and close Excel.
The motions of atoms in globular proteins (e.g., ubiquitin),
referred to as internal dynamics, comprise a wide range of time
scales, from high frequency vibrations about their equilibrium
positions with periods of several femtoseconds to slow collective
motions which require seconds or more, leading to deformations of the
entire protein.
The internal dynamics of these proteins on a picosecond time scale
(high frequency) can be described as a collection of weakly
interacting harmonic oscillators referred to as normal modes. Since
normal modes are formed by linear superposition of a large number of
individual atomic oscillations, it is not surprising that the internal
dynamics of proteins on this time scale has a delocalized character
throughout the protein. The situation is similar to the lattice
vibrations (phonons) in a crystalline solid. Experimentally, there
exist ways to synchronize, through a suitable signal or perturbation,
these normal modes, forcing the system in a so-called (phase) coherent
state, in which normal modes oscillate in phase. The degree of
coherence of the system can be probed with a second signal which
through interference with the coherent normal modes may lead to
resonances, referred to as echoes, which can be detected
experimentally. However, the coherence of atomic motions in proteins
decays through non-linear contributions to forces between atoms. This
decay develops on a time scale 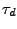 which can be
probed, e.g., by means of temperature echoes, and can be described by
employing MD simulations.
which can be
probed, e.g., by means of temperature echoes, and can be described by
employing MD simulations.
In a temperature echo the coherence of the system is probed by
reassigning the same atomic velocities the system had at an earlier
time and then looking to an echo in the temperature at time 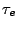 ,
as a result of such reassignment. An example is shown in
Fig. 14. At time
,
as a result of such reassignment. An example is shown in
Fig. 14. At time 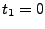 the velocities of all
atoms in the system are quenched; then, at
the velocities of all
atoms in the system are quenched; then, at 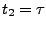 the atomic
velocities are reassigned again (quenched) to their values at time
the atomic
velocities are reassigned again (quenched) to their values at time
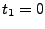 . As a result, a temperature echo, i.e., a sharp dip in
. As a result, a temperature echo, i.e., a sharp dip in
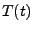 , is detected at a subsequent time
, is detected at a subsequent time 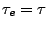 after
after 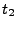 (i.e., at time
(i.e., at time 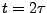 ).
).
In this section, you will employ MD simulations to generate
temperature echoes in ubiquitin by applying the velocity reassignment
just described. By modeling ubiquitin as a large collection of weakly
interacting harmonic oscillators (normal modes), you will find that:
- the dephasing time
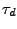 of the oscillators is about one picosecond;
of the oscillators is about one picosecond;
- the temperature echo can be expressed in terms of the temperature
autocorrelation function; and
- the depth
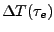 of the echoes decay exponentially
with the delay time
of the echoes decay exponentially
with the delay time 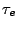 , i.e.,
, i.e.,
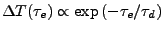 , the exponential decay being
determined by the dephasing time
, the exponential decay being
determined by the dephasing time 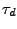 .
.
Figure 14:
Temperature quench echo.
![\begin{figure}\begin{center}
\par
\par
\latex{
\includegraphics[scale=0.5]{pictures/tut_quench-schem}
}
\end{center}
\end{figure}](img124.png) |
First you will generate temperature echoes in MD simulations, and then you will analyze the echoes in the framework of the normal mode approximation.
The phenomenon of temperature echoes has a simple explanation
within the normal modes description of a protein.
The first velocity reassignment enforces phase coherence for the
oscillators. Because of the frequency dispersion of the normal modes
(as well as the deviation from the harmonic approximation) the phase
coherence of the protein will decay in time
with a characteristic dephasing time
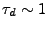 ps.
The second velocity reassignment after a delay time
ps.
The second velocity reassignment after a delay time 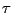 is a
``probing signal'' which will test the degree of coherence of the
system at the instant of time it was applied. The depth of the echo
and the instant of time at which it occurs are quantitative
characteristics of the coherence of the internal dynamics of
proteins.
is a
``probing signal'' which will test the degree of coherence of the
system at the instant of time it was applied. The depth of the echo
and the instant of time at which it occurs are quantitative
characteristics of the coherence of the internal dynamics of
proteins.
In order to generate temperature echoes, one needs to equilibrate
ubiquitin at the desired initial temperature 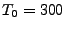 K, e.g., by using
the velocity rescaling method. Once the system is equilibrated, the
thermostat is removed and all the following simulations are carried out
in the microcanonical (NVE) ensemble.
K, e.g., by using
the velocity rescaling method. Once the system is equilibrated, the
thermostat is removed and all the following simulations are carried out
in the microcanonical (NVE) ensemble.
In this section, you will consider two types of temperature
echoes. In the first, you will reassign all atomic velocities to
zero, and in the second, you will reassign the atomic velocities to
a 300 K distribution (the same as the initial temperature of the system)
and the second reassignment will be exactly the same as the first.
The temperature quench echo is obtained by resetting to zero
the velocity of all atoms of the protein at both times 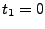 and
and
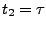 . You should start from the pre-equilibrated protein in
vacuum at
. You should start from the pre-equilibrated protein in
vacuum at 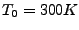 ; the required files are located in the common directory.
; the required files are located in the common directory.
You need to run the simulations in the microcanonical ensemble
(NVE) by using the configuration file equil.conf in the
2-7-echoes/01_equil_NVE directory. The simulation will run for 500
time steps (fs).
- * 1
- Change to the 2-7-echoes/01_equil_NVE directory in a Terminal window.
Let's take a look at some features in the configuration file. You can read the file using WordPad.
- The simulation takes restart files, i.e., the coordinate file and the velocity file, from an equilibration simulation at
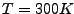 .
.
| # Continuing a job from the restart files |
|
| set inputname ../common/ubi_equil |
|
| binCoordinates $inputname.restart.coor |
|
extendedSystem $inputname.xsc
|
|
- Notice that the temperature line is commented out. The
initial temperature is pre-defined by the initial velocities.
| #temperature $temperature |
|
binvelocities $inputname.restart.vel
|
|
- Since you are running an NVE simulation, there is no temperature
coupling or pressure control.
- As discussed previously, one should use rigidBonds for water in any production simulation since water molecules have been parametrized as rigid molecules. But for the illustration of temperature quench echo, the effect of force field can be negligible. To be simple, the rigidBonds option is turned off.
- * 2
- Close the configuration file and WordPad.
- 3
- Run the Molecular Dynamics simulation
- * 4
- If you do not run the simulation yourself, you will need to obtain the data for the temperature from the provided log file. Copy this log file from the directory example-output/.
copy example-output equil.log . equil.log .
|
|
If you run the simulation yourself, your log file will be generated by NAMD, and you do not need to copy it.
- * 5
- Open VMD by clicking Start
 Programs
Programs  VMD.
VMD.
- * 6
- Once your job is done, you need to get the temperature data from the output file. In the VMD TkCon window (Extensions
 Tk Console), navigate to the 2-7-echoes/01_equil_NVE directory if you are not already there.
Tk Console), navigate to the 2-7-echoes/01_equil_NVE directory if you are not already there.
- * 7
- Get the temperature data at every timestep using our namdstats.tcl script:
| source ../../2-3-energies/namdstats.tcl |
|
data_time TEMP equil.log
|
|
This will write the data into the file TEMP.dat.
- * 8
- You will now calculate the temperature autocorrelation function, which will be used later to analyze the temperature echoes.
- * 9
- A tcl script has been provided for you to calculate the temperature autocorrelation function. Source the script by typing in the VMD TkCon window:
This will put the temperature autocorrelation function in the file auto-corr.dat.
- * 10
- In Excel, click File
 Open
Open , navigate to the directory 2-7-echoes/01_equil_NVE/, and choose the file auto-corr.dat. Make sure the dropdown menu Files of type is set to All Files.
, navigate to the directory 2-7-echoes/01_equil_NVE/, and choose the file auto-corr.dat. Make sure the dropdown menu Files of type is set to All Files.
- * 11
- When the Text Import Wizard appears, choose Delimited for your file type and click Next. Under the category Delimiters, click Tab. The Data Preview window should show your time lag and autocorrelation data separated into two columns. Click Finish. The time lag and autocorrelation function values will appear in Columns A and B, respectively.
- * 12
- Plot the autocorrelation function by clicking Insert
 Chart
Chart , choosing XY (Scatter) as your Chart Type, selecting the last Chart sub-type in the lower-right, and clicking Next. A preview should show that Excel assigned Column A to x-axis and Column B to the y-axis, as we would like. Click Finish.
, choosing XY (Scatter) as your Chart Type, selecting the last Chart sub-type in the lower-right, and clicking Next. A preview should show that Excel assigned Column A to x-axis and Column B to the y-axis, as we would like. Click Finish.
You will now fit the simulated temperature autocorrelation function to a decaying exponential approximation (see the Science Box).
- * 13
- In cell C1, type the following formula:
The value in cell D1 is the decay (temperature autocorrelation) time, 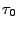 , and we will alter it to obtain a better fit. Enter an initial guess of 1 in cell D1. Then extend the formula in C1 down to cell C26.
, and we will alter it to obtain a better fit. Enter an initial guess of 1 in cell D1. Then extend the formula in C1 down to cell C26.
- * 14
- In the chart, right-click on the temperature autocorrelation function and select Source Data
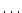 . Click the Series tab and add a new series with Y Values: of Column C, Rows 1-26. and X Values: of Column A. Click OK.
. Click the Series tab and add a new series with Y Values: of Column C, Rows 1-26. and X Values: of Column A. Click OK.
You may want to change the line weight of your functions by right-clicking the lines in your graph and selecting Format Data Series .
.
We have our approximation to the temperature autocorrelation function plotted, but the fit is not optimal. If we change decay time in cell D1, we will see the fit change. We will now determine the optimal decay time.
- * 15
- In cell E1, type the formula =(C1-B1)
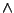 2. Then click and hold the lower-right corner of cell E1 and drag down to row 26 to fill in the error values for each bin.
2. Then click and hold the lower-right corner of cell E1 and drag down to row 26 to fill in the error values for each bin.
- * 16
- Type =sum(E1:E26) into cell F1. This is the total square error for our fit, and it is what we seek to minimize using the Solver tool.
- * 17
- Click Tools
 Solver
Solver . If that option is not present, you will need to add in the Solver tool by clicking Tools
. If that option is not present, you will need to add in the Solver tool by clicking Tools  Add Ins
Add Ins and selecting Solver Add-in from the list.
and selecting Solver Add-in from the list.
- * 18
- In the Solver Parameters window, set the following cell ranges and click Solve:
| Set Target Cell: $F$1 |
|
| Equal To: Min |
|
By Changing Cells: $D$1
|
|
Solver will find the decay time which optimally fits the temperature expression to our raw temperature data. This value will be important for a later analysis of your simulations
- 19
- Modify your chart to display a title, axis labels, etc. if you wish.
Figure 15:
Temperature autocorrelation function from simulation (black) and a decaying exponential approximation (red).
![\begin{figure}\begin{center}
\par
\par
\latex{
\includegraphics[scale=0.5]{pictures/tut_autotempwin}
}
\end{center}
\end{figure}](img134.png) |
- * 20
- Go to the next directory, 02_quencha, by typing in a Terminal window:
cd .. 02_quencha 02_quencha
|
|
- * 21
- You will perform the temperature quenching experiment for the value
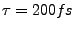 . You are going to quench the temperature (set it to zero), and monitor the recovery of the system as it runs for
. You are going to quench the temperature (set it to zero), and monitor the recovery of the system as it runs for 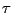 time steps. If you would like to probe other values of
time steps. If you would like to probe other values of 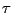 , you should edit your configuration file echo.conf using WordPad, changing the value of tau:
, you should edit your configuration file echo.conf using WordPad, changing the value of tau:
- 22
- Run the Molecular Dynamics simulation
- * 23
- If you do not run the simulation yourself, you will need to obtain the data for the temperature from the provided log file. Copy this log file from the directory example-output/.
copy example-output echo.log . echo.log .
|
|
If you run the simulation yourself, your log file will be generated by NAMD, and you do not need to copy it.
- * 24
- Once your job is done, you need to again get the temperature data from the output file. In the VMD TkCon window, navigate to the 2-7-echoes/02_quencha directory.
- * 25
- Get the temperature data at every timestep using our namdstats.tcl script, which we have already sourced:
This will write the data into the file TEMP.dat.
Now, you will quench the system for the second time.
- * 26
- Change to the directory 03_quenchb in a Terminal window.
Note that the configuration file echo.conf indicates that the simulation will run for 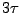 steps: run [expr 3*$tau]
steps: run [expr 3*$tau]
- 27
- Run the Molecular Dynamics simulation
- * 28
- If you do not run the simulation yourself, you will need to obtain the data for the temperature from the provided log file. Copy this log file from the directory example-output/.
copy example-output echo.log . echo.log .
|
|
If you run the simulation yourself, your log file will be generated by NAMD, and you do not need to copy it.
- * 29
- Again, get the temperature data from the output file. In the VMD TkCon window, navigate to the 2-7-echoes/03_quenchb directory and get the temperature data at every timestep using our namdstats.tcl script:
This will write the data into the file TEMP.dat.
- * 30
- In a Terminal window, change the name of this output file so as not to confuse it with the others:
- * 31
- Copy the previous temperature output to this directory, changing their names as you do so:
copy .. 01_equil_NVE 01_equil_NVE TEMP.dat . TEMP.dat . temp1.dat temp1.dat |
|
copy .. 02_quencha 02_quencha TEMP.dat . TEMP.dat . temp2.dat temp2.dat
|
|
- * 32
- Merge the three temperature data files into temp.dat:
| type temp1.dat > temp.dat |
|
| type temp2.dat » temp.dat |
|
type temp3.dat » temp.dat
|
|
You now have the temperature data for the whole temperature quench experiment. You will use Excel to analyze the data.
- * 33
- In Excel, click File
 Open
Open , navigate to the directory 2-7-echoes/03_quenchb/, and choose the file temp.dat. Make sure the dropdown menu Files of type is set to All Files.
, navigate to the directory 2-7-echoes/03_quenchb/, and choose the file temp.dat. Make sure the dropdown menu Files of type is set to All Files.
- * 34
- When the Text Import Wizard appears, choose Delimited for your file type and click Next. Under the category Delimiters, click Tab. The Data Preview window should show your time and temperature data separated into two columns. Click Finish. The time and temperature values will appear in Columns A and B, respectively.
- * 35
- Plot the temperature data by clicking Insert
 Chart
Chart , choosing XY (Scatter) as your Chart Type, selecting the last Chart sub-type in the lower-right, and clicking Next. A preview should show that Excel assigned Column A to x-axis and Column B to the y-axis, as we would like. Click Finish.
, choosing XY (Scatter) as your Chart Type, selecting the last Chart sub-type in the lower-right, and clicking Next. A preview should show that Excel assigned Column A to x-axis and Column B to the y-axis, as we would like. Click Finish.
Note anything unusual? You quenched the temperature twice, and yet you see three drops in temperature! The third one is a temperature echo. See Fig. 16.
Next, you will compare 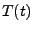 in the vicinity of the echo (
in the vicinity of the echo (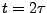 ) obtained from the MD simulation with the theoretical prediction (14) involving the temperature autocorrelation function obtained also from the MD simulations. The degree of agreement between these two results is a measure of the accuracy of the harmonic approximation.
) obtained from the MD simulation with the theoretical prediction (14) involving the temperature autocorrelation function obtained also from the MD simulations. The degree of agreement between these two results is a measure of the accuracy of the harmonic approximation.
- * 36
- You will use a tcl script to calculate the harmonic approximation of the temperature echo, given by Eq. 13. Source the script by typing in the VMD TkCon window:
This will write the data for the harmonic approximation to the file harmonic.dat.
- * 37
- In Excel, view the data by clicking Data
 Get External Data
Get External Data  Import Text File
Import Text File , navigate to the directory 2-7-echoes/03_quenchb/, and choose the file harmonic.dat. Make sure the dropdown menu Files of type is set to All Files.
, navigate to the directory 2-7-echoes/03_quenchb/, and choose the file harmonic.dat. Make sure the dropdown menu Files of type is set to All Files.
- * 38
- When the Text Import Wizard appears, choose Delimited for your file type and click Next. Under the category Delimiters, click Tab. The Data Preview window should show your time and temperature approximation data separated into two columns. Click Finish. When the Import Data window appears, select Existing worksheet: and click cell C1 when asked where you want to put the data. The time and temperature values will appear in Columns C and D, respectively.
- * 39
- Plot the harmonic approximation data by right-clicking on your existing graph and selecting Source Data
 . Click the Series tab and add a series with X Values: of Column C, Rows 1-601. and Y Values: of Column D, Rows 1-601. Click OK.
. Click the Series tab and add a series with X Values: of Column C, Rows 1-601. and Y Values: of Column D, Rows 1-601. Click OK.
- * 40
- You need to find the depth of the echo. Do this by looking at Column B or by entering the following formula into cell E1:
75 is the average temperature after the second quench, and it corresponds to 1/4 of the initial temperature 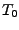 =300K. Note that this formula is designed knowing the echo is between 800 and 1000 fs.
=300K. Note that this formula is designed knowing the echo is between 800 and 1000 fs.
Figure 16:
A comparison of the simulation and the expression from harmonic approximation at the vicinity of the echo.
![\begin{figure}\begin{center}
\par
\par
\latex{
\includegraphics[scale=0.5]{pictures/tut_quenchechowin}
}
\end{center}
\end{figure}](img140.png) |
You have calculated the echo depth for a particular value of the delay time 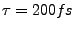 . You may wish to repeat the experiment using other values of
. You may wish to repeat the experiment using other values of 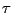 (100-800 fs). (You must alter the harmonic.tcl script.) If this is done and the data is plotted and fitted to a single exponential
(100-800 fs). (You must alter the harmonic.tcl script.) If this is done and the data is plotted and fitted to a single exponential
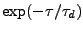 , one obtains the so-called dephasing time
, one obtains the so-called dephasing time 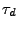 , which is an inherent property of the system.
, which is an inherent property of the system.
Here you will generate a temperature echo by replacing the
velocities of the atoms at time 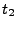 with the ones you assign to
them at time
with the ones you assign to
them at time 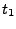 . Moreover, by choosing these velocities according
to the Maxwell-Boltzmann distribution corresponding to
. Moreover, by choosing these velocities according
to the Maxwell-Boltzmann distribution corresponding to 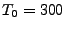 K,
i.e., the temperature of the equilibrated system (
K,
i.e., the temperature of the equilibrated system (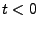 ), there will
be no discontinuities (jumps) in
), there will
be no discontinuities (jumps) in 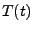 at
at 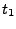 and
and 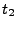 , yet you
will observe a temperature echo at a later time, i.e., a sharp dip in
the temperature at time
, yet you
will observe a temperature echo at a later time, i.e., a sharp dip in
the temperature at time 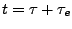 . Your goal is to determine
. Your goal is to determine
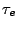 and the depth
and the depth 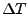 of the echo. To this end, you will
need to follow a similar procedure to the one in the previous
exercise.
of the echo. To this end, you will
need to follow a similar procedure to the one in the previous
exercise.
- * 41
- In a Terminal window, navigate to the directory 04_consta.
- * 42
- Reassign the velocities at
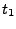 according to a
Maxwell-Boltzmann distribution for a temperature
according to a
Maxwell-Boltzmann distribution for a temperature 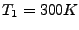 , saving
the reassigned velocities to a file 300.vel.
In order to do this, the following is added to the end of your
configuration file echo.conf:
, saving
the reassigned velocities to a file 300.vel.
In order to do this, the following is added to the end of your
configuration file echo.conf:
These settings will not really run a simulation, but will assign
initial velocities with the desired distribution and save them to
300.vel. Following these, the normal run command is
used to perform a simulation for tau time steps:
- 43
- Run the Molecular Dynamics simulation
- * 44
- If you do not run the simulation yourself, you will need to obtain the data for the temperature from the provided log file. Copy this log file from the directory example-output/.
copy example-output echo.log . echo.log .
|
|
If you run the simulation yourself, your log file will be generated by NAMD, and you do not need to copy it.
- * 45
- In the VMD TkCon window, navigate to the
04_consta directory. Use the script namdstats.tcl
to get the temperature data as before and put it in the file
TEMP.dat. Note that at the beginning there is a duplicate
entry for the first time step. You should delete one of these using
your text editor:
| 500 300.5656 |
|
| 500 300.5656 |
|
| 501 301.0253 |
|
| 502 302.5395 |
|
...
|
|
- * 46
- In a Terminal window, go to the directory 05_constb.
- 47
- For this simulation, you should use the file 300.vel
you generated before as the velocity restart file. This is included
in the configuration file echo.conf as:
velocities ../04_consta/300.vel
|
|
This will reassign the velocities to the exact same distribution
they had at the beginning of the previous simulation. This
simulation will run for 3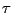 time steps.
time steps.
- 48
- Run the Molecular Dynamics simulation
- * 49
- If you do not run the simulation yourself, you will need to obtain the data for the temperature from the provided log file. Copy this log file from the directory example-output/.
copy example-output echo.log . echo.log .
|
|
If you run the simulation yourself, your log file will be generated by NAMD, and you do not need to copy it.
- * 50
- Again, in the VMD TkCon window, navigate to the
05_constb directory and use the script namdstats.tcl
to output the temperature data to the file TEMP.dat.
- * 51
- In a Terminal window, change the name of this output file and copy the other temperature file to this directory:
| move TEMP.dat temp2.dat |
|
copy .. 04_consta 04_consta TEMP.dat . TEMP.dat . temp1.dat temp1.dat
|
|
- * 52
- Merge the two temperature data files into temp.dat:
| type temp1.dat > temp.dat |
|
type temp2.dat » temp.dat
|
|
- * 53
- Note that there are now two temperature values at 700 fs. You should open the file temp.dat with your text editor and delete one.
- * 54
- Use Excel to plot the temperature data and observe the temperature echo as you did before.
- * 55
- Locate the position of the echo and measure its depth. This time, the depth is measured by:
Echo depth = 300 - Minimum Temperature
|
|
- * 56
- Compare your result with the pre-made results stored in the directory example-output for
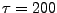 fs. How would you explain your findings?
fs. How would you explain your findings?
- * 57
- You can now close VMD and Excel.


Next: Steered Molecular Dynamics
Up: Analysis
Previous: Equilibrium
namd@ks.uiuc.edu
![\framebox[\textwidth]{
\begin{minipage}[r]{0.9\textwidth}
\noindent{\textbf{Ob...
...s of your simulation, the thermal diffusivity of your system.}
\end{minipage} }](img102.png)
![\framebox[\textwidth]{
\begin{minipage}[r]{0.9\textwidth}
\noindent{\textbf{Ob...
...s of your simulation, the thermal diffusivity of your system.}
\end{minipage} }](img102.png)
![\fbox{
\begin{minipage}{.2\textwidth}
\includegraphics[width=2.3 cm, height=2....
...eft(\frac{n\pi}{R}\right)^2Dt\right].\nonumber
\end{eqnarray}}
\end{minipage} }](img103.png)

![]() .
.
![\begin{figure}\begin{center}
\par
\par
\latex{
\includegraphics[scale=0.5]{pictures/tut_unit02_coolwin}
}
\end{center}
\end{figure}](img105.png)
![]() which can be
probed, e.g., by means of temperature echoes, and can be described by
employing MD simulations.
which can be
probed, e.g., by means of temperature echoes, and can be described by
employing MD simulations.
![]() ,
as a result of such reassignment. An example is shown in
Fig. 14. At time
,
as a result of such reassignment. An example is shown in
Fig. 14. At time ![]() the velocities of all
atoms in the system are quenched; then, at
the velocities of all
atoms in the system are quenched; then, at ![]() the atomic
velocities are reassigned again (quenched) to their values at time
the atomic
velocities are reassigned again (quenched) to their values at time
![]() . As a result, a temperature echo, i.e., a sharp dip in
. As a result, a temperature echo, i.e., a sharp dip in
![]() , is detected at a subsequent time
, is detected at a subsequent time ![]() after
after ![]() (i.e., at time
(i.e., at time ![]() ).
).

![]() ps.
The second velocity reassignment after a delay time
ps.
The second velocity reassignment after a delay time ![]() is a
``probing signal'' which will test the degree of coherence of the
system at the instant of time it was applied. The depth of the echo
and the instant of time at which it occurs are quantitative
characteristics of the coherence of the internal dynamics of
proteins.
is a
``probing signal'' which will test the degree of coherence of the
system at the instant of time it was applied. The depth of the echo
and the instant of time at which it occurs are quantitative
characteristics of the coherence of the internal dynamics of
proteins.
![]() K, e.g., by using
the velocity rescaling method. Once the system is equilibrated, the
thermostat is removed and all the following simulations are carried out
in the microcanonical (NVE) ensemble.
K, e.g., by using
the velocity rescaling method. Once the system is equilibrated, the
thermostat is removed and all the following simulations are carried out
in the microcanonical (NVE) ensemble.
![]() and
and
![]() . You should start from the pre-equilibrated protein in
vacuum at
. You should start from the pre-equilibrated protein in
vacuum at ![]() ; the required files are located in the common directory.
; the required files are located in the common directory.

![]() .
.
![\begin{figure}\begin{center}
\par
\par
\latex{
\includegraphics[scale=0.5]{pictures/tut_autotempwin}
}
\end{center}
\end{figure}](img134.png)

![]() steps: run [expr 3*$tau]
steps: run [expr 3*$tau]

![]() in the vicinity of the echo (
in the vicinity of the echo (![]() ) obtained from the MD simulation with the theoretical prediction (14) involving the temperature autocorrelation function obtained also from the MD simulations. The degree of agreement between these two results is a measure of the accuracy of the harmonic approximation.
) obtained from the MD simulation with the theoretical prediction (14) involving the temperature autocorrelation function obtained also from the MD simulations. The degree of agreement between these two results is a measure of the accuracy of the harmonic approximation.
![\begin{figure}\begin{center}
\par
\par
\latex{
\includegraphics[scale=0.5]{pictures/tut_quenchechowin}
}
\end{center}
\end{figure}](img140.png)
![]() . You may wish to repeat the experiment using other values of
. You may wish to repeat the experiment using other values of ![]() (100-800 fs). (You must alter the harmonic.tcl script.) If this is done and the data is plotted and fitted to a single exponential
(100-800 fs). (You must alter the harmonic.tcl script.) If this is done and the data is plotted and fitted to a single exponential
![]() , one obtains the so-called dephasing time
, one obtains the so-called dephasing time ![]() , which is an inherent property of the system.
, which is an inherent property of the system.
![]() with the ones you assign to
them at time
with the ones you assign to
them at time ![]() . Moreover, by choosing these velocities according
to the Maxwell-Boltzmann distribution corresponding to
. Moreover, by choosing these velocities according
to the Maxwell-Boltzmann distribution corresponding to ![]() K,
i.e., the temperature of the equilibrated system (
K,
i.e., the temperature of the equilibrated system (![]() ), there will
be no discontinuities (jumps) in
), there will
be no discontinuities (jumps) in ![]() at
at ![]() and
and ![]() , yet you
will observe a temperature echo at a later time, i.e., a sharp dip in
the temperature at time
, yet you
will observe a temperature echo at a later time, i.e., a sharp dip in
the temperature at time ![]() . Your goal is to determine
. Your goal is to determine
![]() and the depth
and the depth ![]() of the echo. To this end, you will
need to follow a similar procedure to the one in the previous
exercise.
of the echo. To this end, you will
need to follow a similar procedure to the one in the previous
exercise.

